Решение задач блока Begin 31-40
Решение задач из задачника по программированию М. Э. Абрамяна. Задачи из блока Begin: «Ввод и вывод данных, оператор присваивания».
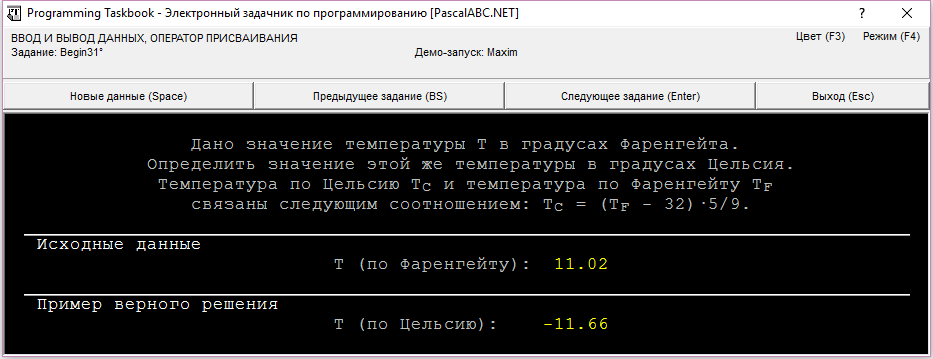
Задача Begin31
Дано значение температуры T в градусах Фаренгейта. Определить значение этой же температуры в градусах Цельсия. Температура по Цельсию TC и температура по Фаренгейту TF связаны следующим соотношением: TC = (TF − 32)·5/9.
uses
PT4;
var
Tf, Tc: real;
begin
Task('Begin31');
read(Tf);
Tc := (Tf - 32) * 5 / 9;
write(Tc);
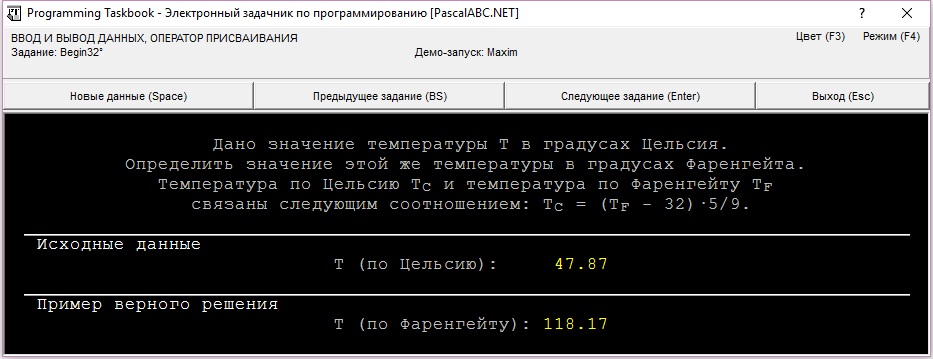
end.Задача Begin32
Дано значение температуры T в градусах Цельсия. Определить значение этой же температуры в градусах Фаренгейта. Температура по Цельсию TC и температура по Фаренгейту TF связаны следующим соотношением: TC = (TF − 32)·5/9.
uses
PT4;
var
Tf, Tc: real;
begin
Task('Begin32');
read(Tc);
Tf := (9 * Tc) / 5 + 32;
write(Tf);
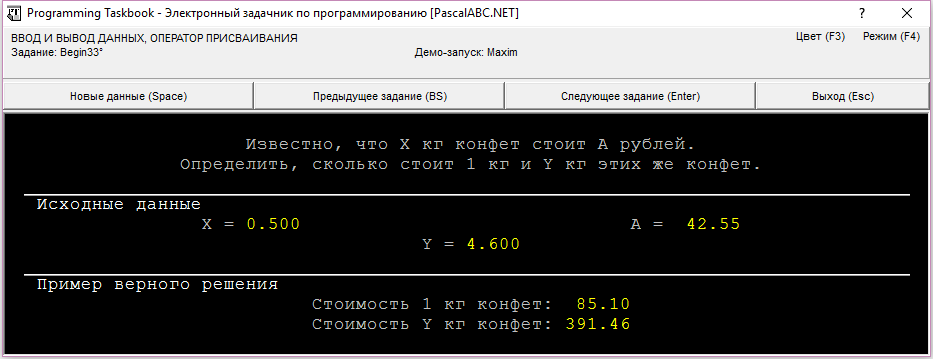
end.Задача Begin33
Известно, что X кг конфет стоит A рублей. Определить, сколько стоит 1 кг и Y кг этих же конфет.
uses
PT4;
var
x, y, a: real;
begin
Task('Begin33');
read(x, a, y);
write(a / x, (a / x) * y);
end.Задача Begin34
Известно, что X кг шоколадных конфет стоит A рублей, а Y кг ирисок стоит B рублей. Определить, сколько стоит 1 кг шоколадных конфет, 1 кг ирисок, а также во сколько раз шоколадные конфеты дороже ирисок.

uses
PT4;
var
x, y, a, b: real;
begin
Task('Begin34');
read(x, a, y, b);
write(a / x, b / y, (a / x) / (b / y));
end.Задача Begin35
Скорость лодки в стоячей воде V км/ч, скорость течения реки U км/ч (U < V). Время движения лодки по озеру T1 ч, а по реке (против течения) — T2 ч. Определить путь S, пройденный лодкой (путь = время · скорость). Учесть, что при движении против течения скорость лодки уменьшается на величину скорости течения.
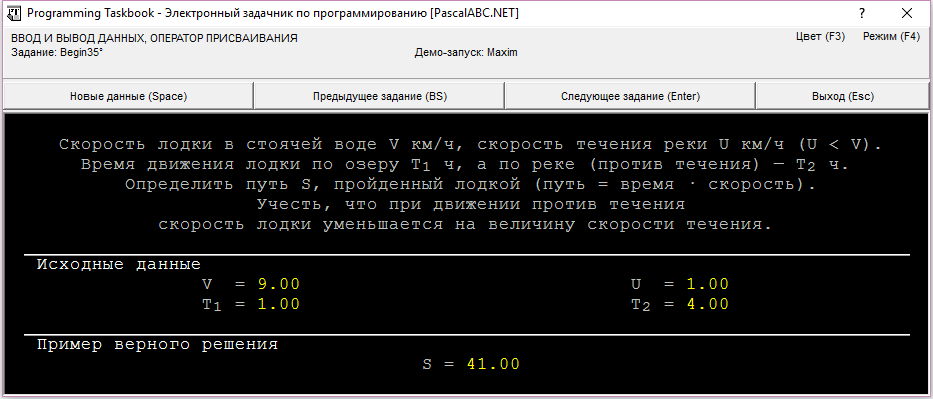
uses
PT4;
var
v, u, t1, t2, s: real;
begin
Task('Begin35');
read(v, u, t1, t2);
s := v * t1 + (v - u) * t2;
write(s);
end.Задача Begin36
Скорость первого автомобиля V1 км/ч, второго — V2 км/ч, расстояние между ними S км. Определить расстояние между ними через T часов, если автомобили удаляются друг от друга, двигаясь в противоположных направлениях. Данное расстояние равно сумме начального расстояния и общего пути, проделанного автомобилями; общий путь = время · суммарная скорость.
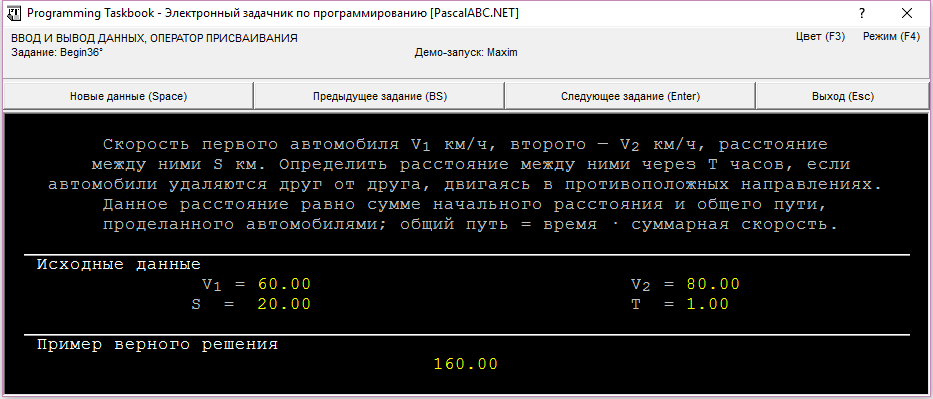
uses
PT4;
var
v1, v2, s, t: real;
begin
Task('Begin36');
read(v1, v2, s, t);
write(s + v1 * t + v2 * t);
end.Задача Begin37
Скорость первого автомобиля V1 км/ч, второго — V2 км/ч, расстояние между ними S км. Определить расстояние между ними через T часов, если автомобили первоначально движутся навстречу друг другу. Данное расстояние равно модулю разности начального расстояния и общего пути, проделанного автомобилями; общий путь = время · суммарная скорость.

uses
PT4;
var
v1, v2, s, t: real;
begin
Task('Begin37');
read(v1, v2, s, t);
write(abs(s - v1 * t - v2 * t));
end.Задача Begin38
Решить линейное уравнение A·x + B = 0, заданное своими коэффициентами A и B (коэффициент A не равен 0).
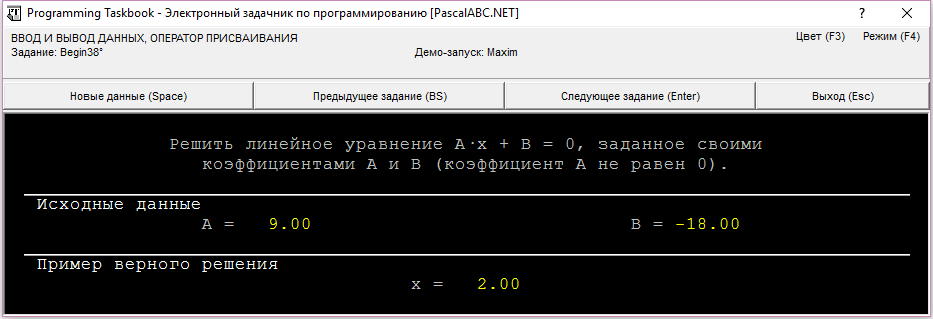
uses
PT4;
var
a, b, x: real;
begin
Task('Begin38');
read(a, b);
x := -b / a;
write(x);
end.Задача Begin39
Найти корни квадратного уравнения A·x2 + B·x + C = 0, заданного своими коэффициентами A, B, C (A > 0), если известно, что дискриминант уравнения положителен. Вывести вначале меньший, а затем больший из найденных корней.
Корни квадратного уравнения находятся по формуле x1, 2 = (−B ± (D)1/2)/(2·A), где D — дискриминант, равный B2 − 4·A·C.
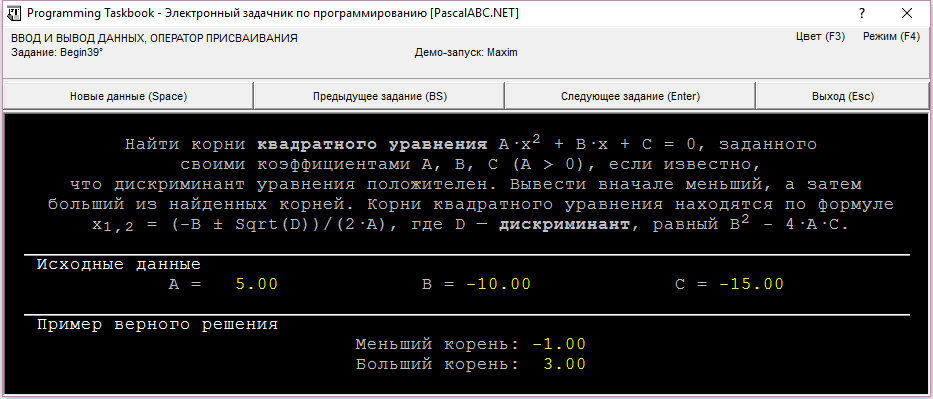
uses
PT4;
var
a, b, c, d, x1, x2: real;
begin
Task('Begin39');
read(a, b, c);
d := sqr(b) - 4 * a * c;
x1 := (-b - sqrt(d)) / (2 * a);
x2 := (-b + sqrt(d)) / (2 * a);
write(x1, x2);
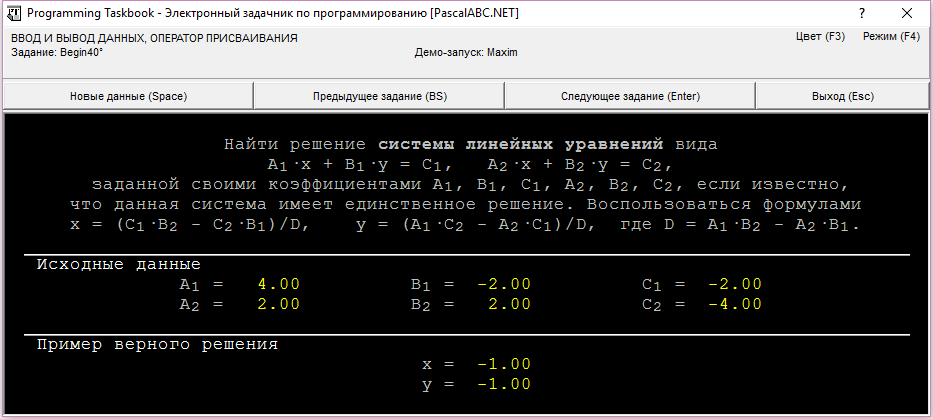
end.Задача Begin40
Найти решение системы линейных уравнений вида
A1·x + B1·y = C1,
A2·x + B2·y = C2,
заданной своими коэффициентами A1, B1, C1, A2, B2, C2, если известно, что данная система имеет единственное решение.
Воспользоваться формулами x = (C1·B2 − C2·B1)/D, y = (A1·C2 − A2·C1)/D, где D = A1·B2 − A2·B1.
uses
PT4;
var
a1, b1, c1, a2, b2, c2, d, x, y: real;
begin
Task('Begin40');
read(a1, b1, c1, a2, b2, c2);
d := a1 * b2 - a2 * b1;
x := (c1 * b2 - c2 * b1) / d;
y := (a1 * c2 - a2 * c1) / d;
write(x, y);
end.